the flix
HCA PA-Technik
Einleitung
Leistungsangaben von Endstufen, aktiven (self-powered) und passiven Lautsprechern sind immer wieder Gegenstand von Diskussionen. Es werden "Peak-Leistungen" und "echte (RMS-)Leistungen" gegenübergestellt, oft mit dem Unterton, dass nur letztere richtig und wichtig seien. Das beschränkt sich nicht auf den PA-Bereich, sondern gilt genauso für den Bereich Studio-Monitore und Instrumentenverstärkung (Gitarre, Bass usw.).Ich möchte hier einen kleinen Rundumschlag anbieten, anhand dessen man Leistungsangaben besser verstehen und einschätzen kann.
2 bewusst provokative Aussagen stelle ich gleich vorne an:
- Peak-Leistungen sind wichtiger, als Dauerleistungen, daher ist deren Angabe gerechtfertigt.
- Leistungen im Allgemeinen sind eine starke Vereinfachung eines komplexen Verhaltens und daher alleine weit weniger wichtig, als oft angenommen.
Was ist (elektrische) Leistung?
Um das zu verstehen, müssen wir uns dem Thema erst einmal auf der theoretischen, elektrotechnischen Seite nähern und die Frage klären, was denn eigentlich elektrische Leistung ist.Die meisten werden die Formel P = U*I (Leistung ist gleich dem Produkt aus Spannung und Stromstärke) schon mal gesehen haben bzw. kennen. Diese kommt von einem sehr einfachen Modell, bestehen aus einer Spannungsquelle und einem Widerstand.
Die Spannungsquelle stellt eine DC-Spannung (Gleichspannung, unveränderlich) bereit.
Durch den Widerstand fließt dann der DC-Strom I = U/R.
Am Widerstand wird die Leistung P = U*I = U²/R = I²*R im wahrsten Sinne des Wortes "verbraten", also in Wärme umgewandelt.
Das ist das erste wichtige, das man sich zum Verständnis merken muss: die "klassische" Leistungsdefinition bezieht sich auf die Wärme, die an der Last (dem Widerstand) entsteht.
Wollen wir die Leistung messen, so müssen 2 der 3 Parameter (U, I, R) ermittelt werden. In der Praxis misst man am besten immer die Spannung über und den Strom durch die Last. Denn Widerstände haben Toleranzen, Temperaturabhängigkeiten und wenn man es genau nimmt, muss man auch die Zuleitungen und Übergangswiderstände beachten. Mit der Strommessung hat man das direkt mit berüchsichtigt.
Machen wir ein Beispiel mit konkreten Zahlen und einen Bild:
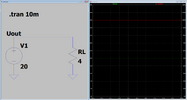
Die Spannung sei 20 V (grüne Kurve), die Last 4 Ohm. Dann ergibt sich eine Leistung von P = 100 W (rote Kurve).
Audio-Leistung traditionell
Was bringt uns diese Definition nun aber im Audio-Bereich? Der wichtige Unterschied ist, dass wir nicht mit DC, sondern mit AC arbeiten, also einem zeitlich nicht konstanten Signal, ganz allgemein gesprochen.Den Rest aus dem einfachen Model können wir jedoch übernehmen. Die Spannungsquelle ist die Endstufe und der Widerstand repräsentiert den Lautsprecher. Letzteres ist oft bekannt, ersteres weniger, jedoch ist es sehr wichtig, das zu verstehen: In aller erster Näherung können wir Endstufen als Spannungsquellen verstehen und die Ausgangsspannung ist deren wichtigster Parameter.
Statt DC gibt unsere Spannungsquelle nun AC aus. Der am einfachsten zu betrachtende Fall ist der eines monofrequenten Signals, oder anders ausgedrückt, eines Sinus.
Schauen wir uns diesen Sinus genauer an. Er ist definiert durch seine Maximalamplitude und seine Frequenz. Die Frequenz ist uns momentan ziemlich egal, für die Beispiele habe ich die üblichen 1 kHz gewählt.
Wir nehmen wieder unsere Last von 4 Ohm, die Maximalspannung beträgt wiederum 20 V. Der Strom durch den Widerstand ist nun selbstverständlich ebenso sinusförmig, wie die Spannung. Berechnen wir nun die Leistung als Multiplikation von Strom und Spannung, so muss diese zwangsläufig zeitabhängig sein. Genau das sehen wir auch hier, die Leistung (rote Kurve) schwankt zwischen 0 W und 100 W.
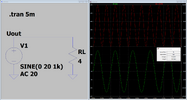
Weitere wichtige Erkenntnis: Wenn wir die Formel aus dem DC-Fall anwenden, so ändert sich die Leistung bei einem AC-Signal über der Zeit.
Mit einer sich ändernden Leistung können wir aber wenig anfangen. Wir erinnern uns an den Zusammenhang zwischen Leistung und Wärme in unserem Modell. Die Wärme, die im Widerstand erzeugt wird, entspricht der mittleren Leistung, nicht der maximalen Leistung. Erstere beträgt in unserem Beispiel 50 W, letztere 100 W.
Nächste wichtige Erkenntnis: Bei einem Sinussignal lassen sich 2 Leistungswerte angeben, eine mittlere, durchschnittliche Leistung und eine Maximalleistung. Es liegt immer ein Faktor 2 zwischen diesen Werten.
Das Sinussignal ist das klassische Messsignal im Audio-Bereich. Messungen damit sind vergleichsweise einfach durchzuführen und auszuwerten. Daher wurde es auch lange Zeit zur Leistungsbestimmung herangezogen. Den Begriff "Sinus-Leistung" findet man noch hin und wieder bei Geräten. Damit ist in der Regel die durchschnittliche Leistung gemeint. Wir betrachten hier also den Fall eines (theoretisch) unendlich langen Sinussignals, das sich nicht verändert.
Audio-Leistung modern
Das Problem mit der Betrachtung von Sinussignalen ist, dass diese keine gute Verallgemeinerung unseres eigentlichen Nutzsignals, der Musik, darstellen. Lange anhaltende Sinussignale treten in der Praxis nur in Sonderfällen auf (manche Synth-Sounds, Feedback, Alarmsirenen). Und selbst dann reden wir über Sekunden und nicht länger. Die überwiegende Mehrzeit der Signal besteht jedoch aus einer wilden Mischung nur kurz anhaltender Sinussignale, oder allgemein ausgedrückt: Rauschen.Rauschsignale haben als Testsignale im Audio-Bereich eine große Verbreitung, weil sie sozusagen das allgemeinste, universellste Musiksignal darstellen.
Ein Rauschen lässt sich durch 3 Parameter beschreiben:
- Maximalamplitude
- Spektrum
- Crestfaktor
Das Spektrum bedarf vermutlich etwas mehr Erklärung. Wir können uns das Rauschen als Kombination beliebig vieler Sinussignale vorstellen. Je nachdem, wie deren individuelle Amplituden ist, ergibt sich ein anderes Spektrum. Sind alle gleich groß, bezeichnet man das Rauschen als "weiß". Sind sie es nicht, handelt es sich um eine gefärbtes Rauschen. Das bekannteste Beispiel dürfte das Pink-Noise (rosa Rauschen) sein. Hierbei nimmt die Amplitude mit 10 dB/Dekade über der Frequenz ab. Der Mensch nimmt so ein Rauschen als spektral gleichmäßig war, wogegen ein weißes Rauschen sehr hochtonlastig klingt.
Weitere standardisierte Rauschsignale sind zusätzlich zur Färbung noch bandbegrenzt, also mit Hoch- und Tiefpass zusätzlich gefiltert. Das Ziel ist immer, ein möglichst repräsentatives Spektrum für Musiksignale zu erreichen. Auf Grund der Vielfältigkeit von Musik ist das natürlich ein eher aussichtsloses Unterfangen, aber eine gewisse Standardisierung ist möglich.
Der Crestfaktor beschreibt das Verhältnis zwischen der Maximalamplitude und der durchschnittlichen Amplitude des Rauschsignals.
Die Maximalamplitude lässt sich einfach ermitteln, aber wie geht das mit der durchschnittlichen? Der einfache Mittelwert kommt nicht in Frage, denn der ist bei einem AC-Signal immer gleich Null (sonst hätte es einen DC-Anteil).
Hierbei kommt eine Abkürzung ins Spiel, die vermutlich jeder schon einmal gehört hat: RMS.
RMS ist die Abkürzung für root-mean-square und bezeichnet ein Berechnungsverfahren. Ein Signal wird quadriert (square), dann wird der Mittelwert über einen bestimmten Zeitbereich gebildet (mean) und schließlich noch die Wurzel gezogen (root), um als Ergebnis wieder dieselbe Einheit zu erhalten. Der RMS-Wert (oder auch Effektivwert) eines AC-Signals ist also sein effektiver Wert über den betrachteten Zeitraum. Der Zusatz mit dem Zeitraum ist ganz wichtig, wie wir noch sehen werden.
Man kann von jedem AC-Signal einen RMS-Wert berechnen, damit natürlich auch von einem Sinus. Wer es mir nicht glaubt, darf es gerne selbst nachrechnen, aber es gilt:
A_max(Sinus) = sqrt(2)*A_rms(Sinus)
Das heißt, die effektive Spannung entspricht der maximalen Spannung geteilt durch Wurzel(2). In unserem vorherigen Beispiel ergibt sich die RMS-Spannung zu ca. 14 V rms (siehe Pop-Up):
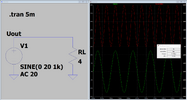
Jetzt verstehen wir auch, woher der Faktor 2 zwischen der maximalen und der mittleren Leistung bei einem Sinussignal kommt:
P = Umax*Imax/2 = Umax/sqrt(2)*Imax/sqrt(2)
Dieser Faktor ist der Crestfaktor, üblicherweise ausgedrückt in dB.
CF_dB = 20*log10(Umax/Urms).
Ein Sinussignal hat also einen Crestfaktor von 3 dB.
Zurück zu unserem beliebigen Musiksignal, aka Rauschen: Die Berechnung des RMS-Werts lassen wir hier sinnvollerweise den Computer machen. Übliche Crestfaktoren sind beispielsweise 12 dB, 9 dB oder 6 dB. Analysiert man Musikstücke, so liegen extrem komprimierte meisten zwischen 6 und 9 dB, Livemusik (Extremfall Klassik) dagegen oft über 12 dB.
Es liegt also nahe, Rauschsignale für die Leistungermittlung von Endstufen heranzuziehen, da diese dem realen Betriebsfall wesentlich näher kommen, also Sinussignale. Für die Messung der Ausgangsleistung einer Endstufe legen wir ein Rauschsignal mit den von uns ausgewählten Parametern an und messen die Spannung über und den Strom durch unsere Last. Für die Leistungsberechnung multiplizieren wir alle Abtastwerte über der Zeit und erhalten damit die Darstellung der momentanen Leistung über der Zeit.
Nur wie werten wir die Ergebnisse aus, wenn wir als Ergebnis eine Leistung erhalten möchten?
Es gibt dafür 3 Ansätze.
Der erste erfolgt analog zum Sinus-Signal, wir ermitteln den Effektivwert (RMS) von Strom und Spannung über dem Zeitfenster der Messung und multiplizieren diese. Damit erhalten wir die mittelere Leistung, die entsprechend der klassischen Definition für die Erwärmung der Last sorgt.
Beim zweiten Ansatz nehmen wir einfach den einmaligen Maximalwert, der bei der Multiplikation von Strom und Spannung über dem Zeitfenster der Messung entsteht. Man kann dies als "einmalige Peak-Leistung" betrachten.
Der dritte Ansatz ist ähnlich zum zweiten, mit dem Unterschied, dass das Ergebnis noch durch 2 geteilt wird. Wer sich wundert, woher dieser Faktor kommt, der sei an den Fall des Sinussignals erinnert. Bei einem Sinus liegt ebenso ein Faktor 2 zwischen der "Peak" und der mittleren Leistung. Man kann diese Leistungsangabe also als "maximale kurzzeitige mittlere Leistung" verstehen.
Diese Leistung ist für uns wichtiger, denn wir interessieren uns nicht für die Leistung, die den Lautsprecher aufheizt (Langzeit), sondern die, die ihn laut macht (Kurzzeit).
Wenn wir uns diese Ansätze anhand konkreter Zahlen veranschaulichen, werden die Unterschiede deutlicher. Nehmen wir ein Rauschen mit 20 V Maximalamplitude, 12 dB Crestfaktor und unsere 4 Ohm Last. Das Testsignal ist in diesem Fall ein Rauschen nach EIA-426B mit 12 dB Crestfaktor mit ca. 5.5 s Länge. Das stellt sich dann so dar (ich habe mir die Umrechnung der Abtastpunkte in Zeit erspart):
Aus den 12 dB Crestfaktor folgt ein Faktor 4 (gerundet) zwischen der Maximalamplitude von Spannung und Strom und ihren RMS-Werten. Das heißt, wir haben 5 V RMS und damit 1.25 A RMS.
Die mittlere Leistung beträgt also 5 V * 1.25 A = 6.25 W.
Die maximale Leistung beträgt 20 V * 5 A = 100 W.
Die kurzzeitige mittlere Leistung beträgt 20 V * 5 A / 2 = 50 W.
Welchen dieser Werte schreibt man nun also in ein Datenblatt?
Der erste ist wenig werbewirksam, scheidet also grundsätzlich aus.
Mit dem zweiten lässt sich dagegen gut werben. Allerdings ist diese Art der Leistungsangabe sehr weit weg von der urspünglichen Leistungsdefinition, die sich auf Wärme zurückführen lässt.
Die dritte ist heute gängige Praxis bei seriösen Angaben. Sie ist vom Prinzip her vergleichbar mit der traditionellen Angabe basierend auf Sinussignalen, wenn man nur eine Periode eines Sinus betrachtet.
Woher weiß ich nun beim Blick auf ein Datenblatt, welches Testsignal und welche Leistungsauswertung herangezogen wird? Solange das Datenblatt sich dazu nicht ausreichend äußert, ist das schwierig zu beurteilen. Ist beispielsweise die maximale Ausgangsspannung angegeben, so kann man die Werte damit kurz plausibilisieren. Leider sind die meisten Datenblattangaben wenig belastbar, weil die wichtigen Randbedingungen fehlen.
So new is always better?
An dieser Stelle kann man sich die berechtigte Frage stellen, warum man dann nicht weiterhin einfach Sinussignale verwendet, wenn das Ergebnis (50 W in unserem Beispiel) dassselbe ist?Der Grund liegt im ersten Ansatz verborgen: Mit einem Rauschsignal ist die langfristige mittlere Leistung durch den höheren Crestfaktor deutlich geringer, als bei einem Sinussignal. An dieser Stelle kommen wir nun zur Frage, was die Ausgangsleistung von Endstufen denn bestimmt und begrenzt.
Den ersten Parameter haben wir schon kennengelernt und ausführlich besprochen: die maximale Ausgangsspannung. Da eine Endstufe in erster Näherung eine Spannungsquelle darstellt, ist die Ausgangsspannung ihr erster Parameter.
Über den Ausgangsstrom muss gesondert gesprochen werden. Bei einer idealen Spannungsquelle ist er unbegrenzt, das heißt, die Last kann beliebig klein werden. So ein Gerät gibt es in der Realität nicht. Den meisten ist sicher bekannt, dass Endstufe mit einer Minimalimpedanz angegeben werden. Daran ist zu erkennen, dass der maximale Strom begrenzt ist bzw. einen fixen Wert hat. Die Gründe dafür sind komplex und ich will nicht zu tief darin einsteigen. Im Prinzip kann man es sich vorstellen, dass der Strom in der Endstufenschaltung Verlustleistung, also Wärme erzeugt, die nur bis zu einem gewissen Punkt abgeführt werden kann. Im Detail kann man hier verschiedene zeitlich unterschiedliche Abläufe unterscheiden (Wärmeübergänge im Transistor, vom Transistorgehäuse auf Kühlkörper, vom Kühlkörper auf die Umgebungsluft usw.). Kurz gesagt, zu viel Strom führt zu zu viel Wärme und dann tritt der magische Rauch aus dem Gerät aus und es funktioniert nicht mehr.
Eine weitere Komponente, die hier zu betrachten ist, ist das Netzteil der Endstufe. Dieses wandelt die Wechselspannung aus dem Stromnetz in eine oder mehrere Gleichspannungen um, die vom eigentlichen Endstufenschaltungsteil dann zur Erzeugung des Audioausgangssignals genutzt werden. Das Netzteil muss ganz grob gesagt die mittlere Ausgangsleistung dauerhaft zur Verfügung stellen können (ich weiß, stark vereinfacht).
Es gibt also mehrere Faktoren in einer Endstufe, die bestimmen, welche kurzfristige und langfristige Ausgangsleistung bereitgestellt werden kann.
Der klassische Designansatz besteht darin, dass die Endstufe eine langfristige mittlere Leistung erzeugen kann, die nur wenig unter ihrer kurzfristigen liegt. Nehmen wir wieder unser Zahlenbeispiel, so hat so eine Endstufe eine maximale Ausgangsspannung von 20 V pk, kann zeitlich unbegrenzt 3.5 A rms ausgeben und das Netzteil kann zeitlich unbegrenzt 50 W liefern. Mit so einer Endstufe ist es egal, ob ich Sinus oder Rauschen zur Leistungsermitlung heranziehe, das Ergebnis wird immer 50 W an 4 Ohm sein.
Jetzt erinnern wir uns aber, das Musik kein Sinus ist. Das heißt, im Betrieb haben wir in den meisten Fällen eine wesentlich niedrigere mittlere Leistung, als die 50 W. Anders ausgedrückt, unsere Kühlung und unser Netzteil werden überhaupt nicht ausgelastet, nur die 20 V pk werden ausgenutzt.
Das ist natürlich nicht im Sinne eines effektiven Designs, denn Kühlung und Netzteil kosten Geld.
Deswegen legt man moderne Endstufen anders aus. Nehmen wir an, wir lassen Kühlung und Netzteil unverändert und rechnen mal aus, mit welcher maximalen Ausgangsspannung wir beides bei einem Crestfaktor von 12 dB voll nutzen.
Bei 12 dB Crestfaktor haben wir einen Faktor 8 zwischen der langfristige und der kurzfristige mittleren Leistung. Kurzfristig sind also 400 W möglich, dafür benötigen wir eine maximale Ausgangsspannung von rund 57 V pk. Dafür muss unsere Schaltung jetzt aber auch ca. 14 A pk liefern können, statt voher nur 5 A pk. Dennoch haben wir so eine wesentlich "größere" Endstufe, ohne alle Teile vergrößert zu haben. Mit realen Musiksignalen nutzen wir nun alle Teile gleichmäßig aus. Der "Nachteil" ist, dass mit kontinuierlichen Sinussignalen trotz mehr Spannung und Strom nicht mehr Leistung herauskommt. Aber wie ich dargelegt habe, ist die Angabe für die Praxis längst nicht so relevant, wie oft angenommen.
Vergleichen wir 2 andere fiktive Endstufen:
Endstufe A
- Umax = 40 V
- Pdauer = 200 W / 4 Ohm
- Pkurz = 200 W / 4 Ohm
- Umax = 80 V
- Pdauer = 100 W / 4 Ohm
- Pkurz = 800 W / 4 Ohm
Endstufe B kann mit kontinuierlichen Sinussignale nur 100 W an 4 Ohm auf Dauer abgeben. Mit Signalen mit hohem Crestfaktor geht jedoch wesentlich mehr, bei 12 dB sind dauerhaft 800 W (Leistungsangabe!) drin.
Endstufe B wird in der überwiegenden Mehrzahl der Fälle mit demselben Lautsprecher lauter spielen, als Endstufe A.
Wir sehen hier wieder den Faktor 8 zwischen Dauer- und Kurzzeitleistung. Diesen Faktor finden wir auch an anderer Stelle, nämlich bei der Angabe der Netzaufnahmeleistung. Hier wird oft "1/8 power" referenziert, was nichts anderes heißt, dass es sich um die durchschnittliche Netzleistung handelt, wenn am Ausgang 1/8 der Kurzzeitleistung dauerhaft abgegeben wird oder anders ausgedrückt, wenn die Endstufe mit einem 12 dB Crestfaktor Rauschen voll ausgesteuert wird. Daran sieht man die Praxisrelevanz dieses Faktors.
Natürlich ist diese Betrachtung zur Veranschaulichung stark idealisiert. In der Realität muss man auch mit Crestfaktoren < 12 dB rechnen und eine Endstufe darauf auslegen. Aber es ist hoffentlich deutlich geworden, dass eine reine Betrachtung von kontinuierlichen Sinussignalen für Audio wenig zielführend ist.
Eben muss man an der Stelle auch hinzufügen, dass die "Freiheit" in der Angabe von Leistungen besonders im extrem preisbewussten Sektor oft stark ausgereizt wird. Es gibt sicher Hersteller, die an Endstufe B 1600 W / 4 Ohm hinschreiben. In den Untiefen des Internets lässt sich auch ein Testbericht der Tools 4 Music einer Hollywood-Endstufe finden, deren Leistungsangaben sich rein gar nicht aus den gemessenen physikalischen Eigenschaften herleiten lassen bzw. nur mit Verrenkungen (P = Upp²/0.5 Ohm).
Aber was ist mit Verzerrungen?
Bei einigen Datenblattangaben zu Leistungen findet sich ein Hinweis auf die dabei gemessenen Verzerrungen, z.B. THD < 1 % THD oder < 0.5 %. Das ist prinzipiell erst mal eine gute Sache. Fehlt diese Angabe, ist dies jedoch nicht gleichbedeutend mit einer unvollständigen Aussage. Es ist schlichtweg so, dass man zur Messung der Verzerrungen Sinussignale verwendet. Eine Messung mit Rauschsignalen ist nicht möglich. Die Sinussignale müssen eine gewisse Länge haben, damit die Messsysteme diese auswerten können. Wir reden hier in der Regel von einigen 100 ms. Wenn eine Endstufe nun so ausgelegt ist, dass sie ihre maximale Leistung nicht so lange halten kann, ist schlicht keine THD-Messung möglich. Es ist also keine Frage, ob die Endstufe verzerrt, sondern ob die Verzerrungen messbar sind.Bei modernen Endstufen ist das Thema Verzerrungen eh meist ein untergeordnetes Problem. Sobald DSP-Limiter zum Schutz der Endstufe verwendet werden und diese sauber parametriert sind, treten Verzerrungen > 1 % THD in der Regel nicht auf.
Vergessen wir den Lautsprecher nicht
Machen wir zum Schluss noch einen weiteren Schritt in Richtung Realität und ersetzen den ohmschen Widerstand durch einen realen Lautsprecher. Dieser besitzt eine komplexe, frequenzabhängige Impedanz. Komplex bedeutet, Strom und Spannung sind nicht zwingend in Phase oder anders ausgedrückt: Bei unseren Beispielen bisher trat der maximale Strom immer zeitgleich mit der maximalen Spannung auf und damit hatten wir automatisch die maximale Peak-Leistung an diesem Zeitpunkt. Bei einem realen Lautsprecher muss das nicht so sein.Die Frequenzabhängigkeit bedeutet, dass die Impedanzangabe sozusagen den worst case darstellt. Diese bezieht sich auf das Minimum über der Frequenz, welches maximal 20 % unter dem angegeben Wert liegen darf. Über weite Frequenzbereiche ist die Impedanz jedoch wesentlich höher. Als Beispiel hier willkührlich ausgewählt der Impedanzverlauf eines geschlossenen 3-Wege Lautsprechers mit nominell 4 Ohm:
Hier fließt über weite Strecken weniger Strom und damit ist auch die Leistung geringer. Allgemein kann man annehmen, dass die durchschnittliche Leistungsabgabe einer Endstufe an einen realen Lautsprecher deutlich geringer ist, als an einen ohmschen Widerstand gleichen (Impedanz)Werts ist.
Das bedeutet, wir brauchen die maximale Leistung einer Endstufe nicht nur zeitlich selten, weil sie nur für die Peaks in der Musik abgerufen wird, sondern auch, weil sie nur abgerufen wird, wenn diese Peaks zusätzlich noch im Impedanzminimum des angeschlossenen Lautsprechers auftreten.
Bisher haben wir die Last, also den Lautsprecher auch so betrachtet, als wäre seine Belastbarkeit zeitlich und frequenztechnisch konstant. Dies ist in der Realität nicht der Fall. Im Allgemeinen hat eine Lautsprecher eine zeit- und frequenzabhängige maximale Eingangsspannung. Aus der frequenzabhängigen Impedanz ergibt sich damit ebenso eine zeit- und frequenzabhängige Belastbarkeit. Dazu muss man sich vor Augen führen, dass der Wirkungsgrad von Lautsprechern in den allermeisten Fällen deutlich unter 5 % liegt. Das heißt, den allergrößten Teil der zugeführten Leistung muss der Lautsprecher in Form von Wärme wieder abführen. Und da sind wir in derselben Situation wie bei der Endstufe selbst, wieviel geht, ist zeitlich unterschiedlich.
Es bringt also nichts, bzw. ist sogar kontraproduktiv, wenn die Endstufe dauerhaft die Leistung liefern kann, die der Lautsprecher nur kurzfristig verträgt.
Das Gebilde aus Endstufenleistung und Lautsprecherbelastbarkeit ist ingesamt sehr komplex und alles andere, als einfach zu verstehen und optimieren. In der Praxis wird es meist so gelöst, dass die Endstufe etwas mehr kann, als der Lautsprecher und diese durch entsprechende zeit- und frequenzabhängige Limiter passend eingebremst wird.
Es hilft auch nicht, dass die Angabe für die Belastbarkeit eines Lautsprechers ebenso vieldeutig ist, wie die der Ausgangsleistung einer Endstufe.
Bottom line
Nach all den Details möchte ich die wichtigsten Aussagen hier zusammenfassen:- Leistungsangaben von Endstufen sind auf vielerlei Arten möglich.
- Es lassen sich technische Argumente für alle Arten finden. Es gibt keine "echte" oder "falsche" Watt (solange gemessen und nicht geraten/gewünscht wird).
- Die traditionelle Art einer Sinus-Dauerleistung hat wenig Praxisrelevanz auf Grund der Eigenschaften von Quellensignalen und Lasten (Musik und Lautsprechern).
- Die Verwendung von Rauschsignalen und die Angabe von kurzzeitigen Leistungen ist besser geeignet, um die Leistungsfähigkeit von Endstufen in der Praxis abzubilden.
- Noch vor der Leistung ist zuerst die maximale Ausgangsspannung einer Endstufe zu betrachten, das sie den besten ersten Hinweis auf den erzielbaren Maximalpegel in Kombination mit einem Lautsprecher liefert.
Ich möchte an dieser Stelle auf den geschätzten Kollegen Anselm Görtz und dessen Tests in der Production Partner verweisen. Er verwendet eine Vielzahl an unterschiedlichen Testsignalen. Hier ist ein (nicht mehr ganz aktueller) Stand aufgeführt, inklusive Motivation:
https://www.production-partner.de/test/verstaerker-leistungsmessung-reloaded/
Dort sind auch Burst-Signale inbegriffen, die ich hier außen vor gelassen habe.
Am Ende lautet also die Antwort auf die Frage "Wie ist das denn jetzt mit der Endstufenleistung?" ehrlicherweise "kommt drauf an". Dennoch hoffe ich, ich konnte mit dieser kleinen Zusammenfassung etwas Licht und Übersicht in das Thema "Endstufenleistung" bringen und so manche Angabe verständlicher machen.
Für fachliche Ergänzungen und Korrekturen (wenn notwendig) bin ich dankbar, ebenso wenn jemand einen Tipp zur besseren Darstellung von Formeln hier im Forum hat.
- Eigenschaft
